Overview¶
E. Pacuit (2019). Voting Methods, Stanford Encyclopedia of Philosophy.
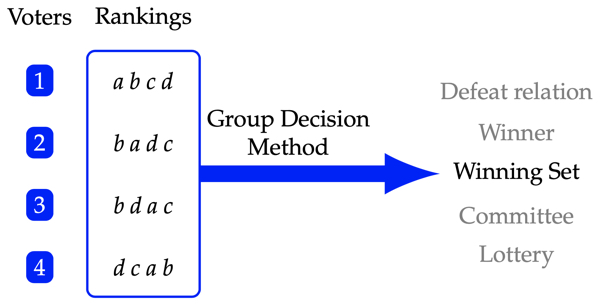
Rankings and Profiles¶
\(V\) is a finite set of voters.
\(X\) is a (typically finite) set of alternatives, or candidates.
A relation \(P\) on \(X\) is a linear order if it is
asymmetric: for all \(x,y\in X\), if \(x\mathrel{P} y\) then it is not the case that \(y\mathrel{P} x\),
transitive: for all \(x,y,z\in X\), if \(x\mathrel{P} y\) and \(y\mathrel{P} z\), then \(x\mathrel{P} z\),
complete: for all \(x,y\in X\), either \(x\mathrel{P} y\) or \(y\mathrel{P} x\).
When \(x\mathrel{P} y\), we say that “\(x\) is strictly preferred to \(y\)”, or that “\(x\) is ranked above \(y\)”.
\(\mathcal{L}(X)\) is the set of all linear orders over the set \(X\).
A profile for \(X\) and \(V\) is a function \(\mathbf{P}\) assigning to \(i\in V\) a linear order \(\mathbf{P}_i\) on \(X\). So, \(a\mathrel{\mathbf{P}_i}b\) means that voter \(i\) strictly prefers candidate \(a\) to \(b\), or that voter \(i\) ranks \(a\) above \(b\). Let \(X(\mathbf{P})\) be the candidates in \(\mathbf{P}\) and \(V(\mathbf{P})\) the voters in \(\mathbf{P}\).
For a profile \(\mathbf{P}\) and candidates \(x,y\in X(\mathbf{P})\), the margin for \(x\) over \(y\) is $\(Margin_{\mathbf{P}}(x,y) = |\{i\mid x\mathrel{\mathbf{P}_i} y\}| - |\{i\mid y\mathrel{\mathbf{P}_i} x\}|\)$
# import the Profile class
from voting.profiles import Profile
num_cands = 3
rankings = [
(0, 1, 2),
(2, 1, 0),
(1, 2, 0)
]
rcounts = [1, 3, 2]
#1 voter with the ranking (0,1,2),
#3 voters with the ranking (2,1,0) and
#2 voters with the ranking (1,2,0)num_cands = 3
prof = Profile(rankings, num_cands, rcounts=rcounts)
print(f"There are {prof.num_voters} voters in the profile.")
# display prof2 - the header is the number of voters with each ranking
prof.display()
There are 6 voters in the profile.
+---+---+---+
| 1 | 3 | 2 |
+---+---+---+
| 0 | 2 | 1 |
| 1 | 1 | 2 |
| 2 | 0 | 0 |
+---+---+---+
rankings = [
(0, 1, 2),
(2, 1, 0),
(1, 2, 0)
]
rcounts = [1, 3, 2]
#1 voter with the ranking (0,1,2),
#2 voters with the ranking (2,1,0) and
#3 voters with the ranking (1,2,0)num_cands = 3
cmap={0:"a", 1:"b", 2:"c"}
prof2 = Profile(rankings, num_cands, rcounts=rcounts, cmap=cmap)
# display prof2 - the header is the number of voters with each ranking
# the candidate names are used in cmap
prof2.display()
+---+---+---+
| 1 | 3 | 2 |
+---+---+---+
| a | c | b |
| b | b | c |
| c | a | a |
+---+---+---+
There are a number of useful methods associated with a Profile. Suppose that \(\mathbf{P}\) is a profile and \(a,b\in X(\mathbf{P})\).
The support for \(a\) over \(b\) is \(|\{i\in V(\mathbf{P})\mid a\mathrel{\mathbf{P}_i}b\}|\).
The margin of \(a\) over \(b\) in \(\mathbf{P}\) is \(Margin_\mathbf{P}(a,b)=|\{i\in V(\mathbf{P})\mid a\mathrel{\mathbf{P}_i}b\}| -|\{i\in V(\mathbf{P})\mid b\mathrel{\mathbf{P}_i} a\}|.\)
Candidate \(a\) is majority preferred to \(b\) when \(Margin_\mathbf{P}(a,b)> 0\).
rankings = [
(0, 1, 2, 3),
(2, 3, 1, 0),
(3, 1, 2, 0),
(1, 2, 0, 3),
(1, 3, 2, 0)
]
num_cands = 4
prof = Profile(rankings, num_cands)
prof.display()
c1 = 2
c2 = 3
print("")
print(f"The candidates are {list(prof.candidates)}")
print(f"support of {c1} over {c2}: ", prof.support(c1,c2))
print(f"support of {c2} over {c1}: ", prof.support(c2, c1))
print(f"Margin({c1},{c2}) = ", prof.margin(c1,c2))
print(f"Margin({c2},{c1}) = ", prof.margin(c2,c1))
print(f"{c1} is majority preferred to {c2} is ", prof.majority_prefers(c1,c2))
print(f"{c2} is majority preferred to {c1} is ", prof.majority_prefers(c2,c1))
print(f"The number of voters that rank {c1} in 1st place is ", prof.num_rank(c1, 1))
print(f"The number of voters that rank {c1} in 2nd place is ", prof.num_rank(c1, 2))
print(f"The size of a strict majority of voters is ", prof.strict_maj_size())
+---+---+---+---+---+
| 1 | 1 | 1 | 1 | 1 |
+---+---+---+---+---+
| 0 | 2 | 3 | 1 | 1 |
| 1 | 3 | 1 | 2 | 3 |
| 2 | 1 | 2 | 0 | 2 |
| 3 | 0 | 0 | 3 | 0 |
+---+---+---+---+---+
The candidates are [0, 1, 2, 3]
support of 2 over 3: 3
support of 3 over 2: 2
Margin(2,3) = 1
Margin(3,2) = -1
2 is majority preferred to 3 is True
3 is majority preferred to 2 is False
The number of voters that rank 2 in 1st place is 1
The number of voters that rank 2 in 2nd place is 1
The size of a strict majority of voters is 3
In addition, there are methods for each of the following:
Condorcet winner: a candidate that is majority preferred to every other candidate (returns None if the Condorcet winner does not exist)
weak Condorcet winner: a list of candidates that are not majority preferred by any other candidate (returns None if no such candidate exists)
Condorcet loser: a candidate that is majority dispreferred by every other candidate (returns None if the Condorcet loser does not exist)
Plurality scores: a dictionary associating with each candidate its plurality score
Borda scores: a dictionary associating with each candidate its Borda score
rankings = [
(0, 1, 2, 3),
(2, 3, 1, 0),
(3, 1, 2, 0),
(1, 2, 0, 3),
(1, 3, 2, 0)
]
num_cands = 4
prof = Profile(rankings, num_cands)
prof.display()
print("")
print(f"The plurality scores are ", prof.plurality_scores())
print(f"The Borda scores are ", prof.borda_scores())
print(f"The Condorcet winner is ", prof.condorcet_winner())
print(f"The weak Condorcet winner is ", prof.weak_condorcet_winner())
print(f"The Condorcet loser is ", prof.condorcet_loser())
+---+---+---+---+---+
| 1 | 1 | 1 | 1 | 1 |
+---+---+---+---+---+
| 0 | 2 | 3 | 1 | 1 |
| 1 | 3 | 1 | 2 | 3 |
| 2 | 1 | 2 | 0 | 2 |
| 3 | 0 | 0 | 3 | 0 |
+---+---+---+---+---+
The plurality scores are {0: 1, 1: 2, 2: 1, 3: 1}
The Borda scores are {0: 4, 1: 11, 2: 8, 3: 7}
The Condorcet winner is 1
The weak Condorcet winner is [1]
The Condorcet loser is 0
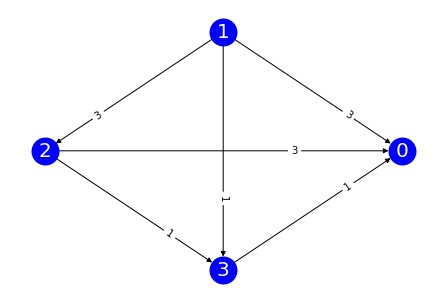
Margin Graphs¶
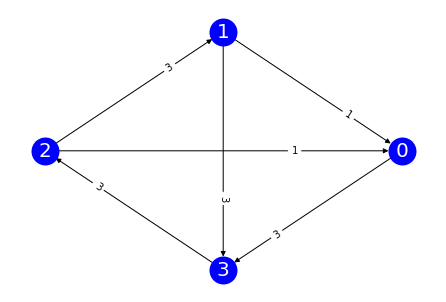
The margin graph of a profile \(\mathbf{P}\) is a weighted directed graph where the nodes are the candidates and there is an edge from \(a\) to \(b\) when \(Margin_{\mathbf{P}}(a,b)>0,\) weighted by \(Margin_{\mathbf{P}}(a,b)\).
A margin graph for a Profile object is a networkx object.
rankings = [
(0, 1, 2, 3),
(2, 3, 1, 0),
(3, 1, 2, 0),
(1, 2, 0, 3),
(1, 3, 2, 0)
]
num_cands = 4
prof = Profile(rankings, num_cands)
prof.display()
mg = prof.margin_graph()
# mg is a networkx object
print(type(mg))
print("The nodes are the candidates ", mg.nodes)
print("The edges are the majority relations ", mg.edges)
print("The weights are the margins \n", "\n ".join([f"Edge {e}: {mg.get_edge_data(*e)}" for e in mg.edges]))
# display the margin graph
prof.display_margin_graph()
+---+---+---+---+---+
| 1 | 1 | 1 | 1 | 1 |
+---+---+---+---+---+
| 0 | 2 | 3 | 1 | 1 |
| 1 | 3 | 1 | 2 | 3 |
| 2 | 1 | 2 | 0 | 2 |
| 3 | 0 | 0 | 3 | 0 |
+---+---+---+---+---+
<class 'networkx.classes.digraph.DiGraph'>
The nodes are the candidates [0, 1, 2, 3]
The edges are the majority relations [(1, 0), (1, 2), (1, 3), (2, 0), (2, 3), (3, 0)]
The weights are the margins
Edge (1, 0): {'weight': 3}
Edge (1, 2): {'weight': 3}
Edge (1, 3): {'weight': 1}
Edge (2, 0): {'weight': 3}
Edge (2, 3): {'weight': 1}
Edge (3, 0): {'weight': 1}
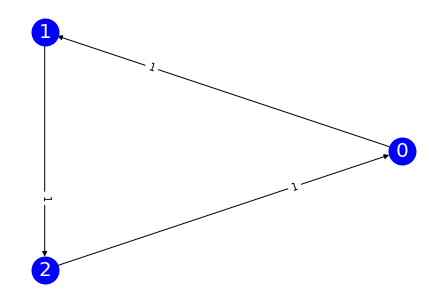
Majority Cycle¶
rankings = [
(0, 1, 2),
(1, 2, 0),
(2, 0, 1)
]
num_cands = 3
prof = Profile(rankings, num_cands)
prof.display()
prof.display_margin_graph()
+---+---+---+
| 1 | 1 | 1 |
+---+---+---+
| 0 | 1 | 2 |
| 1 | 2 | 0 |
| 2 | 0 | 1 |
+---+---+---+
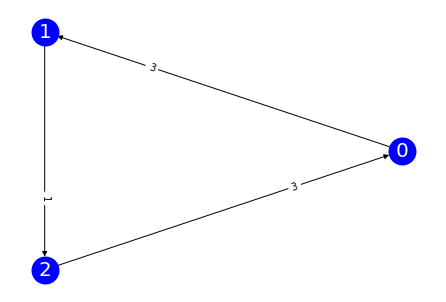
rankings = [
(0, 1, 2),
(1, 2, 0),
(2, 0, 1)
]
rcounts = [2, 2, 3]
num_cands = 3
prof = Profile(rankings, num_cands, rcounts = rcounts)
prof.display()
prof.display_margin_graph()
+---+---+---+
| 2 | 2 | 3 |
+---+---+---+
| 0 | 1 | 2 |
| 1 | 2 | 0 |
| 2 | 0 | 1 |
+---+---+---+
rankings = [
(1, 0, 3, 2),
(0, 1, 3, 2),
(3, 0, 2, 1),
(0, 3, 2, 1),
(2, 1, 0, 3),
(1, 3, 2, 0),
(2, 3, 0, 1),
(3, 2, 0, 1)
]
rcounts = [2, 1, 1, 1, 3, 1, 1, 1]
num_cands = 4
prof = Profile(rankings, num_cands, rcounts = rcounts)
prof.display()
prof.display_margin_graph()
+---+---+---+---+---+---+---+---+
| 2 | 1 | 1 | 1 | 3 | 1 | 1 | 1 |
+---+---+---+---+---+---+---+---+
| 1 | 0 | 3 | 0 | 2 | 1 | 2 | 3 |
| 0 | 1 | 0 | 3 | 1 | 3 | 3 | 2 |
| 3 | 3 | 2 | 2 | 0 | 2 | 0 | 0 |
| 2 | 2 | 1 | 1 | 3 | 0 | 1 | 1 |
+---+---+---+---+---+---+---+---+
Voting Methods¶
A voting method is a function \(F\) mapping profiles (in the domain of \(F\)) to non-empty set of candidates: \(\varnothing \neq F(\mathbf{P})\subseteq X(\mathbf{P})\)
from voting.voting_methods import *
# all_vms is an list of all the voting methods that have been implemented
# all_vms_mg is a list of all voting methods that accept margin graphs as input
vms = [
plurality,
borda,
hare,
coombs,
]
for vm in vms:
print(vm.name)
print(vm.__doc__)
Plurality
A plurality winnner a candidate that is ranked first by the most voters
Borda
A Borda winner is a candidate with the larget Borda score.
The Borda score of the candidates is calculated as follows: If there are $m$ candidates, then
the Borda score of candidate $c$ is \sum_{r=1}^{m (m - r) * Rank(c,r)$ where $Rank(c,r)$ is the
number of voters that rank candidate $c$ in position $r$.
Ranked Choice
If there is a majority winner then that candidate is the ranked choice winner
If there is no majority winner, then remove all candidates that are ranked first by the fewest
number of voters. Continue removing candidates with the fewest number first-place votes until
there is a candidate with a majority of first place votes.
Note: If there is more than one candidate with the fewest number of first-place votes, then *all*
such candidates are removed from the profile.
Note: We typically refer to this method as "Ranked Choice", but it also known as "Hare" or "IRV"
Coombs
If there is a majority winner then that candidate is the Coombs winner
If there is no majority winner, then remove all candidates that are ranked last by the greatest
number of voters. Continue removing candidates with the most last-place votes until
there is a candidate with a majority of first place votes.
Note: If there is more than one candidate with the most number of last-place votes, then *all*
such candidates are removed from the profile.
rankings = [
(0, 1, 2, 3),
(2, 3, 1, 0),
(3, 1, 2, 0),
(1, 2, 0, 3),
(1, 3, 2, 0)
]
num_cands = 4
prof = Profile(rankings, num_cands)
prof.display()
for vm in vms:
print(f"{vm.name}: {vm(prof)}")
+---+---+---+---+---+
| 1 | 1 | 1 | 1 | 1 |
+---+---+---+---+---+
| 0 | 2 | 3 | 1 | 1 |
| 1 | 3 | 1 | 2 | 3 |
| 2 | 1 | 2 | 0 | 2 |
| 3 | 0 | 0 | 3 | 0 |
+---+---+---+---+---+
Plurality: [1]
Borda: [1]
Ranked Choice: [1]
Coombs: [1]
rankings = [(0,1,2), (1,2,0), (2,0,1)]
rcounts = [2,2,1]
num_cands = 3
prof = Profile(rankings, num_cands, rcounts=rcounts)
prof.display()
for vm in vms:
print(f"{vm.name}: {vm(prof)}")
+---+---+---+
| 2 | 2 | 1 |
+---+---+---+
| 0 | 1 | 2 |
| 1 | 2 | 0 |
| 2 | 0 | 1 |
+---+---+---+
Plurality: [0, 1]
Borda: [1]
Ranked Choice: [0]
Coombs: [1]
