Contents

Games on a Network

Fix a 2x2 game. Each agent plays this game with her neighbors in a network.

At each step:

  1. One agent (the focal agent) is chosen at random to adopt a new strategy

  2. The focal agent chooses a new strategy based on how well her neighbors perform in the game:

    • imitation: imitate the neighbor with the highest total score for that round

    • prob_imitation: select a neighbor to imitate proportional to the average payouts

from mesa import Model, Agent
from mesa.batchrunner import BatchRunner
from mesa.time import RandomActivation
from mesa.space import SingleGrid
from mesa.datacollection import DataCollector
import random

import nashpy as nash
import matplotlib.pyplot as plt
from IPython.display import clear_output
from ipywidgets import widgets, interact, interact_manual
import seaborn as sns
import numpy as np
import pandas
import tqdm.notebook as tqdm
import seaborn as sns

sns.set()

# Create some games:

A = np.array([[3, 0], [4, 1]])
B = np.array([[3, 4], [0, 1]])
pd = nash.Game(A, B)
#print(pd)

A = np.array([[3, 0], [6, 1]])
B = np.array([[3, 6], [0, 1]])
pd2 = nash.Game(A, B)
#print(pd2)

A = np.array([[1, 0], [0, 1]])
B = np.array([[1, 0], [0, 1]])
coord = nash.Game(A, B)
#print(coord)

A = np.array([[2, 0], [0, 1]])
B = np.array([[2, 0], [0, 1]])
hilo = nash.Game(A, B)
#print(hilo)


A = np.array([[2, 0], [0, 1]])
B = np.array([[1, 0], [0, 2]])
bos = nash.Game(A, B)
#print(bos)

A = np.array([[4, 1], [3, 2]])
B = np.array([[4, 3], [1, 2]])
sh = nash.Game(A, B)
#print(sh)

A = np.array([[9, 0], [8, 7]])
B = np.array([[9, 8], [0, 7]])
sh2 = nash.Game(A, B)
#print(str(sh2))

# fix two strategies
S1 = np.array([1, 0])
S2 = np.array([0, 1])

STRATS = {
    "S1": S1,
    "S2": S2
}

class Player(Agent):
    '''
    A player for a game 
    '''
    def __init__(self, unique_id, pos, model, strat):

        super().__init__(unique_id, model)
        self.pos = pos
        self.strat = strat # fixed strategy to play in the game 

    def average_payout(self):
        '''find the average payout when playing the game against all neighbors'''
        neighbors = self.model.grid.neighbor_iter(self.pos)
        return np.average([self.model.game[STRATS[self.strat], STRATS[n.strat]][0] for n in neighbors])
    
    def total_payout(self):
        '''find the total payout when playing the game against all neighbors'''
        neighbors = self.model.grid.neighbor_iter(self.pos)
        return np.sum([self.model.game[STRATS[self.strat], STRATS[n.strat]][0] for n in neighbors])
    
    def step(self):
        pass

class GameLatticeModel(Model):
    '''
    Play a fixed game on a lattice.
    '''
    def __init__(self, height, width, game, bias_S1, num_changes_per_step, mutation, update_type):
        
        self.height = height
        self.width = width
        self.game = game
        self.bias_S1 = bias_S1
        self.update_type = update_type
        self.num_changes_per_step = num_changes_per_step
        self.mutation = mutation
        
        self.schedule = RandomActivation(self)
        self.grid = SingleGrid(height, width, torus=True)
        
        self.datacollector = DataCollector(
             {"Percent S1": lambda m: np.sum([1 for a in m.schedule.agents 
                                              if   a.strat ==  "S1"]) / m.schedule.get_agent_count()}             )
        self.running = True
        
        # Set up agents
        agent_id = 0
        for cell in self.grid.coord_iter():
            _,x,y = cell
            strat = "S1" if random.random() < self.bias_S1 else "S2"
            agent = Player(agent_id, (x, y), self, strat)
            self.grid.position_agent(agent, x=x, y=y)
            self.schedule.add(agent)
            agent_id += 1
        
    def step(self):
        for i in range(self.num_changes_per_step):
            
            # choose a random agent
            focal_agent = np.random.choice(self.schedule.agents)
            
            # find all the neighbors of the agent
            neighbors = self.grid.get_neighbors(focal_agent.pos, moore=True)
            
            
            if self.update_type == 'imitator':
                # imitate most successful neighbor
                total_payouts  = {a: a.total_payout() for a in neighbors}

                max_payout = max(total_payouts.values())

                strat_to_imitate = [a.strat for a in total_payouts.keys() if total_payouts[a] == max_payout][0]

            if self.update_type == 'prob_imitator':
                
                # get the average payouts for each neighbor
                average_payouts = [a.average_payout() for a in neighbors]
                total_average_payouts = np.sum(average_payouts)
                
                # probabilities for each neighbor
                neighbor_probs = [n.average_payout() / total_average_payouts for n in neighbors]
                
                # probabilistically imitate most successful neighbor 
                strat_to_imitate = np.random.choice(neighbors, 1, p=neighbor_probs)[0].strat
            
            
            # mutations
            other_strat = "S2" if strat_to_imitate == "S1" else "S1"
            
            if random.random() < self.mutation:
                focal_agent.strat = other_strat
            else: 
                focal_agent.strat = strat_to_imitate
            
            self.datacollector.collect(self)
            
            self.schedule.steps += 1
        
        # stop running if all agents have the same strategy

        if all([a.strat == "S1" for a in self.schedule.agents]) or all([a.strat == "S2" for a in self.schedule.agents]):
            self.running=False
            
                        

height, width = 20, 20 
game = sh
bias_S1 = 0.5
mutation = 0.0
update_type = 'imitator'
num_changes_per_step = 1
model = GameLatticeModel(height, width, 
                         game, bias_S1, 
                         num_changes_per_step, 
                         mutation, update_type)


for i in tqdm.tqdm(range(1000)):
# initialize the model
    model.step()
    if not model.running:
        break
        
model_out = model.datacollector.get_model_vars_dataframe()
model_out.plot();
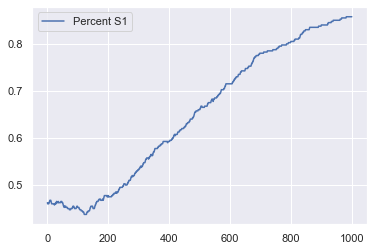
../_images/02b-games-local-interaction_5_1.png

Exploring the Parameter Space

def get_percentS1(m):
    '''
    Find the % of agents playing the strategy S1.
    '''
    
    return np.sum([1 for a in m.schedule.agents
                   if a.strat == "S1"]) / m.schedule.get_agent_count()

variable_params = {"mutation": [0.0, 0.1, 0.2, 0.3]}
fixed_params =  {"height": 20, 
                 "width": 20, 
                 "bias_S1": 0.5, 
                 "update_type": "imitator", 
                 "game": sh,
                 "num_changes_per_step": 1} 
model_reporters = {"PercentS1": get_percentS1}
param_sweep = BatchRunner(GameLatticeModel, 
                          variable_params, 
                          fixed_params, 
                          iterations=5, 
                          max_steps=1000, 
                          model_reporters=model_reporters, 
                          display_progress=False)

param_sweep.run_all()

df = param_sweep.get_model_vars_dataframe()
df
mutation Run PercentS1 height width bias_S1 update_type game num_changes_per_step
0 0.0 0 0.9125 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
1 0.0 1 0.9275 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
2 0.0 2 0.9100 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
3 0.0 3 0.8650 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
4 0.0 4 0.9525 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
5 0.1 5 0.8250 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
6 0.1 6 0.8450 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
7 0.1 7 0.8050 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
8 0.1 8 0.8025 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
9 0.1 9 0.8025 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
10 0.2 10 0.7400 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
11 0.2 11 0.6700 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
12 0.2 12 0.7025 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
13 0.2 13 0.6675 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
14 0.2 14 0.6825 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
15 0.3 15 0.6600 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
16 0.3 16 0.5525 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
17 0.3 17 0.5725 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
18 0.3 18 0.5725 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1
19 0.3 19 0.5750 20 20 0.5 imitator Bi matrix game with payoff matrices:\n\nRow pl... 1 
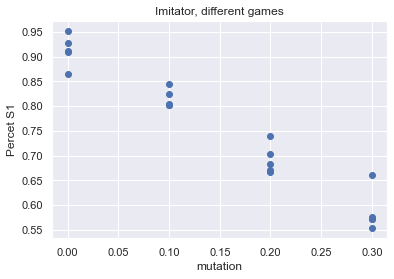
plt.scatter(df.mutation, df.PercentS1)
plt.title("Imitator, different games")
plt.ylabel("Percet S1")
plt.xlabel("mutation")
plt.grid(True)
../_images/02b-games-local-interaction_9_0.png 
variable_params = {"game": [pd, pd2, coord, hilo, bos, sh, sh2]}
fixed_params =  {"height": 20, 
                 "width": 20, 
                 "bias_S1": 0.5, 
                 "update_type": "prob_imitator", 
                 "mutation": 0.0,
                 "num_changes_per_step": 1} 
model_reporters = {"PercentS1": get_percentS1}
param_sweep = BatchRunner(GameLatticeModel, 
                          variable_params, 
                          fixed_params, 
                          iterations=10, 
                          max_steps=1000, 
                          model_reporters=model_reporters, 
                          display_progress=False)
param_sweep.run_all()

df = param_sweep.get_model_vars_dataframe()
df
game Run PercentS1 height width bias_S1 update_type mutation num_changes_per_step
0 Bi matrix game with payoff matrices:\n\nRow pl... 0 0.2375 20 20 0.5 prob_imitator 0.0 1
1 Bi matrix game with payoff matrices:\n\nRow pl... 1 0.2500 20 20 0.5 prob_imitator 0.0 1
2 Bi matrix game with payoff matrices:\n\nRow pl... 2 0.2900 20 20 0.5 prob_imitator 0.0 1
3 Bi matrix game with payoff matrices:\n\nRow pl... 3 0.2200 20 20 0.5 prob_imitator 0.0 1
4 Bi matrix game with payoff matrices:\n\nRow pl... 4 0.2425 20 20 0.5 prob_imitator 0.0 1
... ... ... ... ... ... ... ... ... ...
65 Bi matrix game with payoff matrices:\n\nRow pl... 65 0.1550 20 20 0.5 prob_imitator 0.0 1
66 Bi matrix game with payoff matrices:\n\nRow pl... 66 0.2450 20 20 0.5 prob_imitator 0.0 1
67 Bi matrix game with payoff matrices:\n\nRow pl... 67 0.1575 20 20 0.5 prob_imitator 0.0 1
68 Bi matrix game with payoff matrices:\n\nRow pl... 68 0.2875 20 20 0.5 prob_imitator 0.0 1
69 Bi matrix game with payoff matrices:\n\nRow pl... 69 0.2050 20 20 0.5 prob_imitator 0.0 1

70 rows × 9 columns

def convert_game_string(gstr):
    
    if gstr == str(pd):
        return "PD"
    if gstr == str(pd2):
        return "PD2"
    if gstr == str(coord):
        return "Coord"
    if gstr == str(hilo):
        return "HiLo"
    if gstr == str(bos):
        return "BoS"
    if gstr == str(sh):
        return "SH"
    if gstr == str(sh2):
        return "SH2"
    return gstr

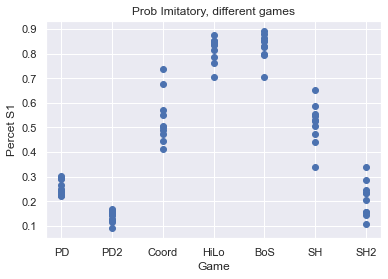
plt.scatter([convert_game_string(str(g)) for g in df.game], df.PercentS1)
plt.title("Prob Imitatory, different games")
plt.ylabel("Percet S1")
plt.xlabel("Game")
plt.grid(True)
../_images/02b-games-local-interaction_11_0.png 
variable_params = {"game": [pd, pd2, coord, hilo, bos, sh, sh2], 
                   "update_type": ["imitator", "prob_imitator"]}
fixed_params =  {"height": 20, 
                 "width": 20, 
                 "bias_S1": 0.5, 
                 "mutation": 0.0,
                 "num_changes_per_step": 1} 
model_reporters = {"PercentS1": get_percentS1}
param_sweep = BatchRunner(GameLatticeModel, 
                          variable_params, 
                          fixed_params, 
                          iterations=10, 
                          max_steps=1000, 
                          model_reporters=model_reporters, 
                          display_progress=False)

param_sweep.run_all()

df = param_sweep.get_model_vars_dataframe()
df
game update_type Run PercentS1 height width bias_S1 mutation num_changes_per_step
0 Bi matrix game with payoff matrices:\n\nRow pl... imitator 0 0.0550 20 20 0.5 0.0 1
1 Bi matrix game with payoff matrices:\n\nRow pl... imitator 1 0.0425 20 20 0.5 0.0 1
2 Bi matrix game with payoff matrices:\n\nRow pl... imitator 2 0.0450 20 20 0.5 0.0 1
3 Bi matrix game with payoff matrices:\n\nRow pl... imitator 3 0.0825 20 20 0.5 0.0 1
4 Bi matrix game with payoff matrices:\n\nRow pl... imitator 4 0.1125 20 20 0.5 0.0 1
... ... ... ... ... ... ... ... ... ...
135 Bi matrix game with payoff matrices:\n\nRow pl... prob_imitator 135 0.1675 20 20 0.5 0.0 1
136 Bi matrix game with payoff matrices:\n\nRow pl... prob_imitator 136 0.1875 20 20 0.5 0.0 1
137 Bi matrix game with payoff matrices:\n\nRow pl... prob_imitator 137 0.1825 20 20 0.5 0.0 1
138 Bi matrix game with payoff matrices:\n\nRow pl... prob_imitator 138 0.2525 20 20 0.5 0.0 1
139 Bi matrix game with payoff matrices:\n\nRow pl... prob_imitator 139 0.2950 20 20 0.5 0.0 1

140 rows × 9 columns

def convert_game_string(gstr):
    
    if gstr == str(pd):
        return "PD"
    if gstr == str(pd2):
        return "PD2"
    if gstr == str(coord):
        return "Coord"
    if gstr == str(hilo):
        return "HiLo"
    if gstr == str(bos):
        return "BoS"
    if gstr == str(sh):
        return "SH"
    if gstr == str(sh2):
        return "SH2"
    return gstr

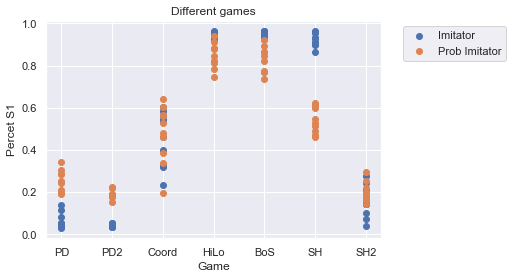
plt.scatter([convert_game_string(str(g)) for g in df[df["update_type"] == "imitator"].game],  
            df[df["update_type"] == "imitator"].PercentS1, label="Imitator")
plt.scatter([convert_game_string(str(g)) for g in df[df["update_type"] == "prob_imitator"].game], 
            df[df["update_type"] == "prob_imitator"].PercentS1, label="Prob Imitator")
plt.title("Different games")
plt.ylabel("Percet S1")
plt.xlabel("Game")
plt.legend(bbox_to_anchor=(1.05, 1))
plt.grid(True)
../_images/02b-games-local-interaction_13_0.png

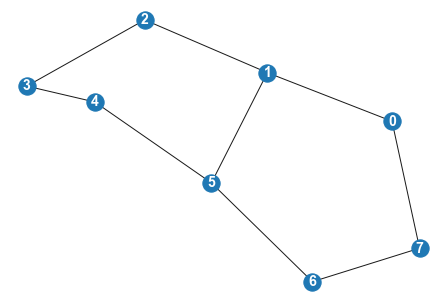
Games on Graphs

import networkx as nx

G = nx.Graph()

G.add_nodes_from([0,1,2,3,4,5,6,7])
G.add_edges_from([(0,1), (5, 1),  (1,2), (2,3), (3,4), (4,5),(5,6), (6,7), (7,0)])

nx.draw(G, with_labels = True, font_color="white", font_size=14,font_weight='bold')
../_images/02b-games-local-interaction_16_0.png 
from mesa.space import NetworkGrid

# fix two strategies
S1 = np.array([1, 0])
S2 = np.array([0, 1])

STRATS = {
    "S1": S1,
    "S2": S2
}


class Player(Agent):
    '''
    A player for a game 
    '''
    def __init__(self, unique_id, pos, model, strat):

        super().__init__(unique_id, model)
        self.pos = pos
        self.strat = strat # fixed strategy to play in the game 

    def average_payout(self):
        '''find the average payout when playing the game against all neighbors'''
            
        neighbors_nodes = [a for a in self.model.network.get_neighbors(self.pos)]
            
        neighbors = [a for a in self.model.schedule.agents if a.pos in neighbors_nodes]
        return np.average([self.model.game[STRATS[self.strat], STRATS[n.strat]][0] for n in neighbors])
    
    def total_payout(self):
        '''find the total payout when playing the game against all neighbors'''
        neighbors_nodes = [a for a in self.model.network.get_neighbors(self.pos)]
            
        neighbors = [a for a in self.model.schedule.agents if a.pos in neighbors_nodes]
        return np.sum([self.model.game[STRATS[self.strat], STRATS[n.strat]][0] for n in neighbors])

    
    
class GameNetworkModel(Model):
    '''
    Play a fixed game on a lattice.
    '''
    def __init__(self,  game, bias_S1,  mutation, update_type, network):
        
        self.height = height
        self.width = width
        self.game = game
        self.bias_S1 = bias_S1
        self.update_type = update_type
        self.num_changes_per_step = num_changes_per_step
        self.mutation = mutation
        
        self.schedule = RandomActivation(self)
        self.network = NetworkGrid(network)
        
        self.datacollector = DataCollector(
             {"Percent S1": lambda m: np.sum([1 for a in m.schedule.agents 
                                              if  a.strat == "S1"]) / m.schedule.get_agent_count()}             )
        self.running = True
        
        # Set up agents
        agent_id = 0
        for n in network.nodes:
            
            strat = "S1" if random.random() < self.bias_S1 else "S2"
            agent = Player(agent_id, n, self, strat)
            self.network.place_agent(agent, n)
            self.schedule.add(agent)
            agent_id += 1
        
    def step(self):
        for i in range(self.num_changes_per_step):
            
            # choose a random agent
            focal_agent = np.random.choice(self.schedule.agents)
            
            # find all the neighbors of the agent
            
            neighbors_nodes = [a for a in self.network.get_neighbors(focal_agent.pos)]
            
            neighbors = [a for a in self.schedule.agents if a.pos in neighbors_nodes]
            if self.update_type == 'imitator':
                # imitate most successful neighbor
                total_payouts  = {a: a.total_payout() for a in neighbors}

                max_payout = max(total_payouts.values())

                strat_to_imitate = [a.strat for a in total_payouts.keys() if total_payouts[a] == max_payout][0]

            if self.update_type == 'prob_imitator':
                
                # get the average payouts for each neighbor
                average_payouts = [a.average_payout() for a in neighbors]
                total_average_payouts = np.sum(average_payouts)
                
                # probabilities for each neighbor
                neighbor_probs = [n.average_payout() / total_average_payouts for n in neighbors]
                
                # probabilistically imitate most successful neighbor 
                strat_to_imitate = np.random.choice(neighbors, 1, p=neighbor_probs)[0].strat
            
            
            # mutations
            other_strat = "S2" if strat_to_imitate == "S1" else "S1"
            
            if random.random() < self.mutation:
                focal_agent.strat = other_strat
            else: 
                focal_agent.strat = strat_to_imitate
            
            self.datacollector.collect(self)
            
            # stop running if all agents have the same strategy
            if len(list(set([a.strat for a in self.schedule.agents]))) == 1:
                self.running=False
            
            

height, weight = 10, 10
bias_S1 = 0.5  
mutation = 0
update_type = "prob_imitator"
game = sh

model = GameNetworkModel(game, 
                         bias_S1, 
                         mutation, 
                         update_type, 
                         G)

for i in tqdm.tqdm(range(100)):
# initialize the model
    model.step()
    if not model.running:
        break
        
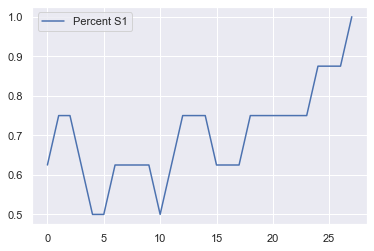
model_out = model.datacollector.get_model_vars_dataframe()
model_out.plot();
../_images/02b-games-local-interaction_19_1.png 
G = nx.cycle_graph(100)

nx.draw(G, pos=nx.circular_layout(G), 
        with_labels = True, 
        font_color="white", 
        font_size=14,
        font_weight='bold')

bias_S1 = 0.5  
mutation = 0
update_type = "imitator"
game = pd

model = GameNetworkModel(game, 
                         bias_S1, 
                         mutation, 
                         update_type, 
                         G)
for i in tqdm.tqdm(range(500)):
# initialize the model
    model.step()
    if not model.running:
        break
        
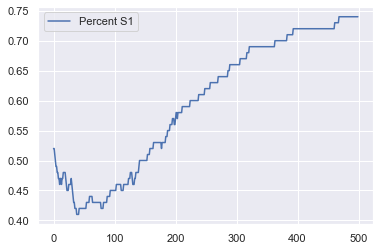
model_out = model.datacollector.get_model_vars_dataframe()
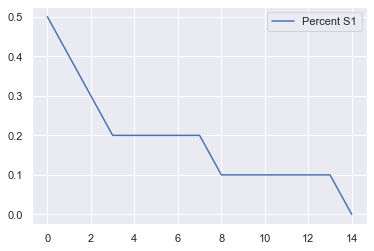
model_out.plot();
../_images/02b-games-local-interaction_20_1.png ../_images/02b-games-local-interaction_20_2.png 
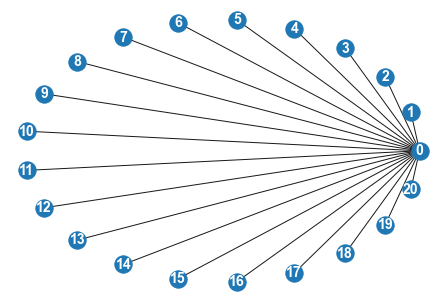
G = nx.star_graph(20)

nx.draw(G, pos=nx.circular_layout(G), with_labels = True, font_color="white", font_size=14,font_weight='bold')

bias_S1 = 0.5  
mutation = 0
update_type = "imitator"
game = sh

model = GameNetworkModel(game, 
                         bias_S1, 
                         mutation, 
                         update_type, 
                         G)
for i in tqdm.tqdm(range(500)):
# initialize the model
    model.step()
    if not model.running:
        break
        
model_out = model.datacollector.get_model_vars_dataframe()
model_out.plot();
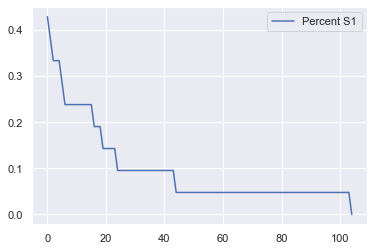
../_images/02b-games-local-interaction_21_1.png ../_images/02b-games-local-interaction_21_2.png 
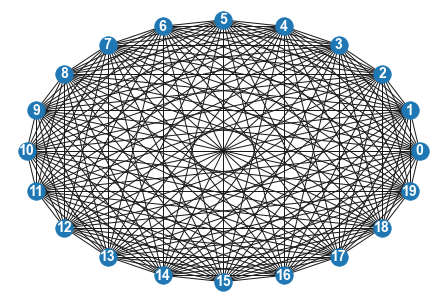
G = nx.complete_graph(20)

nx.draw(G, pos=nx.circular_layout(G), with_labels = True, font_color="white", font_size=14,font_weight='bold')
bias_S1 = 0.5
mutation = 0
update_type = "imitator"
game = coord

model = GameNetworkModel(game, 
                         bias_S1, 
                         mutation, 
                         update_type, 
                         G)
for i in tqdm.tqdm(range(500)):
# initialize the model
    model.step()
    if not model.running:
        break
        
model_out = model.datacollector.get_model_vars_dataframe()
model_out.plot();
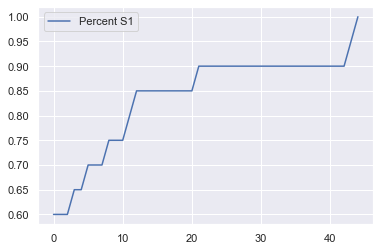
../_images/02b-games-local-interaction_22_1.png ../_images/02b-games-local-interaction_22_2.png 
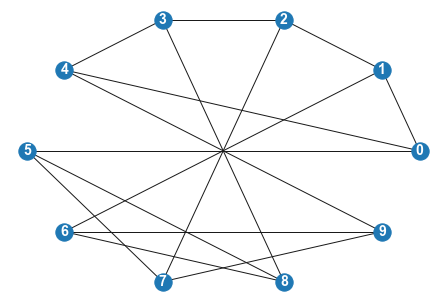
G = nx.petersen_graph()

nx.draw(G, pos=nx.circular_layout(G), with_labels = True, font_color="white", font_size=14,font_weight='bold')
bias_S1 = 0.5  
mutation = 0
update_type = "imitator"
game = pd2

model = GameNetworkModel(game, 
                         bias_S1, 
                         mutation, 
                         update_type, 
                         G)
for i in tqdm.tqdm(range(500)):
# initialize the model
    model.step()
    if not model.running:
        break
        
model_out = model.datacollector.get_model_vars_dataframe()
model_out.plot();
../_images/02b-games-local-interaction_23_1.png ../_images/02b-games-local-interaction_23_2.png 
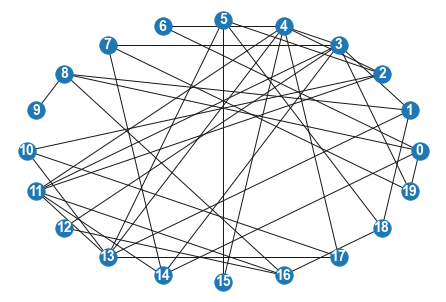
G = nx.erdos_renyi_graph(20, 0.2)

nx.draw(G, pos=nx.circular_layout(G), with_labels = True, font_color="white", font_size=14,font_weight='bold')
bias_S1 = 0.5  
mutation = 0
update_type = "imitator"
game = pd

model = GameNetworkModel(game, 
                         bias_S1, 
                         mutation, 
                         update_type, 
                         G)
for i in tqdm.tqdm(range(500)):
# initialize the model
    model.step()
    if not model.running:
        break
        
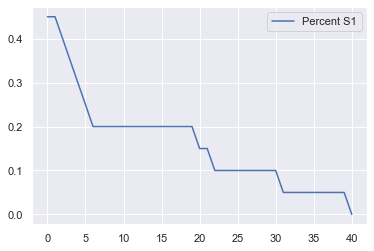
model_out = model.datacollector.get_model_vars_dataframe()
model_out.plot();
../_images/02b-games-local-interaction_24_1.png ../_images/02b-games-local-interaction_24_2.png

Further Reading

  1. M. Jackson and Y. Zenou (2014). Games on Networks, In: Handbook of Game Theory Vol. 4, edited by Peyton Young and Shmuel Zamir, Elsevier Science.

  2. P. Forber and R. Smead (2014). The evolution of fairness through spite, Proceedings of the Royal Society B: Biological Sciences 281 (1780).

  3. P. Forber and R. Smead (2014). An Evolutionary Paradox for Prosocial Behavior, The Journal of Philosophy, 11:3, pp. 151 - 166

  4. J. McKenzie Alexander and P. Vanderschraaf (2005). Follow the Leader: Local Interactions with Influence Neighborhoods, Philosophy of Science, pp. 86 - 113.

Introduction to Game Theory Justice and Bargaining